43. Job Search II: Search and Separation #

In addition to what’s in Anaconda, this lecture will need the following libraries:

!pip install quantecon

43.1. Overview #

Previously we looked at the McCall job search model [McCall, 1970] as a way of understanding unemployment and worker decisions.

One unrealistic feature of that version of the model was that every job is permanent.

In this lecture, we extend the model by introducing job separation.

Once separation enters the picture, the agent comes to view

the loss of a job as a capital loss, and
a spell of unemployment as an investment in searching for an acceptable job

The other minor addition is that a utility function will be included to make worker preferences slightly more sophisticated.

We’ll need the following imports

import matplotlib.pyplot as plt
import numpy as np
import jax
import jax.numpy as jnp
from typing import NamedTuple
from quantecon.distributions import BetaBinomial
from myst_nb import glue

43.2. The Model #

The model is similar to the baseline McCall job search model.

It concerns the life of an infinitely lived worker and

the opportunities he or she (let’s say he to save one character) has to work at different wages
exogenous events that destroy his current job
his decision making process while unemployed

The worker can be in one of two states: employed or unemployed.

He wants to maximize

(43.1)#\[{\mathbb E} \sum_{t=0}^\infty \beta^t u(y_t)\]

At this stage the only difference from the baseline model is that we’ve added some flexibility to preferences by introducing a utility function \(u\).

It satisfies \(u'> 0\) and \(u'' < 0\).

Wage offers \(\{ w_t \}\) are IID with common distribution \(q\).

The set of possible wage values is denoted by \(\mathbb W\).

43.2.1. Timing and Decisions#

At the start of each period, the agent can be either

unemployed or
employed at some existing wage level \(w\).

At the start of a given period, the current wage offer \(w_t\) is observed.

If currently employed, the worker

receives utility \(u(w)\) and
is fired with some (small) probability \(\alpha\).

If currently unemployed, the worker either accepts or rejects the current offer \(w_t\).

If he accepts, then he begins work immediately at wage \(w_t\).

If he rejects, then he receives unemployment compensation \(c\).

The process then repeats.

Note

We do not allow for job search while employed—this topic is taken up in a later lecture.

43.3. Solving the Model #

We drop time subscripts in what follows and primes denote next period values.

Let

\(v_e(w)\) be maximum lifetime value accruing to a worker who enters the current period employed with existing wage \(w\)
\(v_u(w)\) be maximum lifetime value accruing to a worker who who enters the current period unemployed and receives wage offer \(w\).

Here maximum lifetime value means the value of (43.1) when the worker makes optimal decisions at all future points in time.

As we now show, obtaining these functions is key to solving the model.

43.3.1. The Bellman Equations#

We recall that, in the original job search model, the value function (the value of being unemployed with a given wage offer) satisfied a Bellman equation.

Here this function again satisfies a Bellman equation that looks very similar.

(43.2)#\[ v_u(w) = \max \left\{ v_e(w), \, u(c) + \beta \sum_{w' \in \mathbb W} v_u(w') q(w') \right\}\]

The difference is that the value of accepting is \(v_e(w)\) rather than \(w/(1-\beta)\).

We have to make this change because jobs are not permanent.

Accepting transitions the worker to employment and hence yields reward \(v_e(w)\).

Rejecting leads to unemployment compensation and unemployment tomorrow.

Equation (43.2) expresses the value of being unemployed with offer \(w\) in hand as a maximum over the value of two options: accept or reject the current offer.

The function \(v_e\) also satisfies a Bellman equation:

(43.3)#\[ v_e(w) = u(w) + \beta \left[ (1-\alpha)v_e(w) + \alpha \sum_{w' \in \mathbb W} v_u(w') q(w') \right]\]

Note

This equation differs from a traditional Bellman equation because there is no max.

There is no max because an employed agent has no choices.

Nonetheless, in keeping with most of the literature, we also refer to it as a Bellman equation.

Equation (43.3) expresses the value of being employed at wage \(w\) in terms of

current reward \(u(w)\) plus
discounted expected reward tomorrow, given the \(\alpha\) probability of being fired

As we will see, equations (43.3) and (43.2) provide enough information to solve for both \(v_e\) and \(v_u\).

Once we have them in hand, we will be able to make optimal choices.

43.3.2. The Reservation Wage#

Let

(43.4)#\[ h := u(c) + \beta \sum_{w' \in \mathbb W} v_u(w') q(w')\]

This is the continuation value for an unemployed agent (the value of rejecting the current offer).

If we know \(v_u\) then we can easily compute \(h\).

From (43.2), we see that an unemployed agent accepts current offer \(w\) if \(v_e(w) \geq h\).

This means precisely that the value of accepting is higher than the value of rejecting.

It is clear that \(v_e\) is (at least weakly) increasing in \(w\), since the agent is never made worse off by a higher wage offer.

Hence, we can express the optimal choice as accepting wage offer \(w\) if and only if \(w \geq \bar w\), where the reservation wage \(\bar w\) is the first wage level \(w\) such that

\[ v_e(w) \geq h \]

43.4. Code #

Let’s now implement a solution method based on the two Bellman equations.

43.4.1. Set Up#

In the code, you’ll see that we use a class to store the various parameters and other objects associated with a given model.

This helps to tidy up the code and provides an object that’s easy to pass to functions.

The default utility function is a CRRA utility function

def u(c, γ):
    return (c**(1 - γ) - 1) / (1 - γ)

Also, here’s a default wage distribution, based around the BetaBinomial distribution:

n = 60                                  # n possible outcomes for w
w_default = jnp.linspace(10, 20, n)     # wages between 10 and 20
a, b = 600, 400                         # shape parameters
dist = BetaBinomial(n-1, a, b)          # distribution
q_default = jnp.array(dist.pdf())       # probabilities as a JAX array

Here’s our model class for the McCall model with separation.

class Model(NamedTuple):
    α: float = 0.2              # job separation rate
    β: float = 0.98             # discount factor
    γ: float = 2.0              # utility parameter (CRRA)
    c: float = 6.0              # unemployment compensation
    w: jnp.ndarray = w_default  # wage outcome space
    q: jnp.ndarray = q_default  # probabilities over wage offers

43.4.2. Operators#

To iterate on the Bellman equations, we define two operators, one for each value function.

These operators take the current value functions as inputs and return updated versions.

def T_u(model, v_u, v_e):
    """
    Apply the unemployment Bellman update rule.

    """
    α, β, γ, c, w, q = model
    h = u(c, γ) + β * (v_u @ q)
    return jnp.maximum(v_e, h)

def T_e(model, v_u, v_e):
    """
    Apply the employment Bellman update rule.

    """
    α, β, γ, c, w, q = model
    v_e_new = u(w, γ) + β * ((1 - α) * v_e + α * (v_u @ q))
    return v_e_new

43.4.3. Iteration#

Here’s our iteration routine, which alternates between updating \(v_u\) and \(v_e\) until convergence.

We iterate until successive realizations are closer together than some small tolerance level.

def solve_full_model(
        model,
        tol: float=1e-6,
        max_iter: int=1_000,
    ):
    """
    Solves for both value functions v_u and v_e iteratively.

    """
    α, β, γ, c, w, q = model
    i = 0
    error = tol + 1
    v_e = v_u = w / (1 - β)

    while i < max_iter and error > tol:
        v_u_next = T_u(model, v_u, v_e)
        v_e_next = T_e(model, v_u, v_e)
        error_u = jnp.max(jnp.abs(v_u_next - v_u))
        error_e = jnp.max(jnp.abs(v_e_next - v_e))
        error = jnp.max(jnp.array([error_u, error_e]))
        v_u = v_u_next
        v_e = v_e_next
        i += 1

    return v_u, v_e

43.4.4. Computing the Reservation Wage#

Now that we can solve for both value functions, let’s compute the reservation wage.

Recall from above that the reservation wage \(\bar w\) solves \(v_e(\bar w) = h\), where \(h\) is the continuation value defined in (43.4).

Let’s compare \(v_e\) and \(h\) to see what they look like.

We’ll use the default parameterizations found in the code above.

model = Model()
α, β, γ, c, w, q = model
v_u, v_e = solve_full_model(model)
h = u(c, γ) + β * (v_u @ q)

fig, ax = plt.subplots()
ax.plot(w, v_e, 'b-', lw=2, alpha=0.7, label='$v_e$')
ax.plot(w, [h] * len(w), 'g-', lw=2, alpha=0.7, label='$h$')
ax.set_xlim(min(w), max(w))
ax.legend()
plt.show()

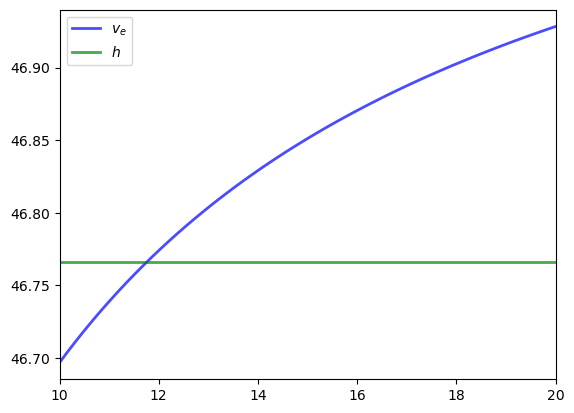
_images/e31c9d66847c95a5a1e63e8bc3705a73c657f39173ba0cbc4817dee911849945.png

The value \(v_e\) is increasing because higher \(w\) generates a higher wage flow conditional on staying employed.

The reservation wage is the \(w\) where these lines meet.

Let’s compute this reservation wage explicitly:

def compute_reservation_wage_full(model):
    """
    Computes the reservation wage using the full model solution.
    """
    α, β, γ, c, w, q = model
    v_u, v_e = solve_full_model(model)
    h = u(c, γ) + β * (v_u @ q)
    # Find the first w such that v_e(w) >= h
    accept = v_e >= h
    i = jnp.argmax(accept)
    w_bar = jnp.where(jnp.any(accept), w[i], jnp.inf)
    return w_bar

w_bar_full = compute_reservation_wage_full(model)
print(f"Reservation wage (full model): {w_bar_full:.4f}")

Reservation wage (full model): 11.8644

43.5. A Simplifying Transformation #

The approach above works, but iterating over two vector-valued functions is computationally expensive.

Let’s return to the key equations and see if we can simplify them to reduce the problem to a single scalar equation.

(This process will be analogous to our second pass at the plain vanilla McCall model, where we reduced the Bellman equation to an equation in an unknown scalar value, rather than an unknown vector.)

First, recall \(h\) as defined in (43.4).

Using \(h\), we can now write (43.2) as

\[ v_u(w) = \max \left\{ v_e(w), \, h \right\} \]

or, shifting time forward one period

\[ \sum_{w' \in \mathbb W} v_u(w') q(w') = \sum_{w' \in \mathbb W} \max \left\{ v_e(w'), \, h \right\} q(w') \]

Using (43.4) again now gives

(43.5)#\[h = u(c) + \beta \sum_{w' \in \mathbb W} \max \left\{ v_e(w'), \, h \right\} q(w')\]

Finally, from (43.4) we have

\[ \sum_{w' \in \mathbb W} v_u(w') q(w') = \frac{h - u(c)}{\beta} \]

so (43.3) can now be rewritten as

(43.6)#\[v_e(w) = u(w) + \beta \left[ (1-\alpha)v_e(w) + \alpha \frac{h - u(c)}{\beta} \right]\]

43.5.1. Simplifying to a Single Equation#

We can simplify further by solving (43.6) for \(v_e\) as a function of \(h\).

Rearranging (43.6) gives

\[ v_e(w) = u(w) + \beta(1-\alpha)v_e(w) + \alpha(h - u(c)) \]

\[ v_e(w) - \beta(1-\alpha)v_e(w) = u(w) + \alpha(h - u(c)) \]

Solving for \(v_e(w)\):

(43.7)#\[v_e(w) = \frac{u(w) + \alpha(h - u(c))}{1 - \beta(1-\alpha)}\]

Substituting this into (43.5) yields

(43.8)#\[h = u(c) + \beta \sum_{w' \in \mathbb W} \max \left\{ \frac{u(w') + \alpha(h - u(c))}{1 - \beta(1-\alpha)}, \, h \right\} q(w')\]

This is a single scalar equation in \(h\).

43.5.2. Solving the Bellman Equations#

We’ll use the same iterative approach to solving the Bellman equations that we adopted in the first job search lecture.

In this case we only need to iterate on the single scalar equation (43.8).

The iteration rule is

(43.9)#\[h_{n+1} = u(c) + \beta \sum_{w' \in \mathbb W} \max \left\{ \frac{u(w') + \alpha(h_n - u(c))}{1 - \beta(1-\alpha)}, \, h_n \right\} q(w')\]

starting from some initial condition \(h_0\).

Once convergence is achieved, we can compute \(v_e\) from (43.7).

(It is possible to prove that (43.9) converges via the Banach contraction mapping theorem.)

43.6. Implementation #

First, we define a function to compute \(v_e\) from \(h\) using (43.7).

def compute_v_e(model, h):
    " Compute v_e from h using the closed-form expression. "
    α, β, γ, c, w, q = model
    return (u(w, γ) + α * (h - u(c, γ))) / (1 - β * (1 - α))

Now we implement the iteration on \(h\) only:

def update_h(model, h):
    " One update of the scalar h. "
    α, β, γ, c, w, q = model
    v_e = compute_v_e(model, h)
    h_new = u(c, γ) + β * (jnp.maximum(v_e, h) @ q)
    return h_new

Using this iteration rule, we can write our model solver.

@jax.jit
def solve_model(model, tol=1e-5, max_iter=2000):
    " Iterates to convergence on the Bellman equations. "

    def cond(loop_state):
        h, i, error = loop_state
        return jnp.logical_and(error > tol, i < max_iter)

    def update(loop_state):
        h, i, error = loop_state
        h_new = update_h(model, h)
        error_new = jnp.abs(h_new - h)
        return h_new, i + 1, error_new

    # Initialize
    h_init = u(model.c, model.γ) / (1 - model.β)
    i_init = 0
    error_init = tol + 1
    init_state = (h_init, i_init, error_init)

    final_state = jax.lax.while_loop(cond, update, init_state)
    h_final, _, _ = final_state

    # Compute v_e from the converged h
    v_e_final = compute_v_e(model, h_final)

    return v_e_final, h_final

Here’s a function compute_reservation_wage that takes an instance of Model and returns the associated reservation wage.

def compute_reservation_wage(model):
    """
    Computes the reservation wage of an instance of the McCall model
    by finding the smallest w such that v_e(w) >= h.

    """
    # Find the first i such that v_e(w_i) >= h and return w[i]
    # If no such w exists, then w_bar is set to np.inf
    v_e, h = solve_model(model)
    accept = v_e >= h
    i = jnp.argmax(accept)   # take first accept index
    w_bar = jnp.where(jnp.any(accept), model.w[i], jnp.inf)
    return w_bar

Let’s verify that this simplified approach gives the same answer as the full model:

w_bar_simplified = compute_reservation_wage(model)
print(f"Reservation wage (simplified): {w_bar_simplified:.4f}")
print(f"Reservation wage (full model): {w_bar_full:.4f}")
print(f"Difference: {abs(w_bar_simplified - w_bar_full):.6f}")

Reservation wage (simplified): 11.8644
Reservation wage (full model): 11.8644
Difference: 0.000000

As we can see, both methods produce essentially the same reservation wage, but the simplified method is much more efficient.

Next we will investigate how the reservation wage varies with parameters.

43.7. Impact of Parameters #

In each instance below, we’ll show you a figure and then ask you to reproduce it in the exercises.

43.7.1. The Reservation Wage and Unemployment Compensation#

First, let’s look at how \(\bar w\) varies with unemployment compensation.

In the figure below, we use the default parameters in the Model class, apart from c (which takes the values given on the horizontal axis)

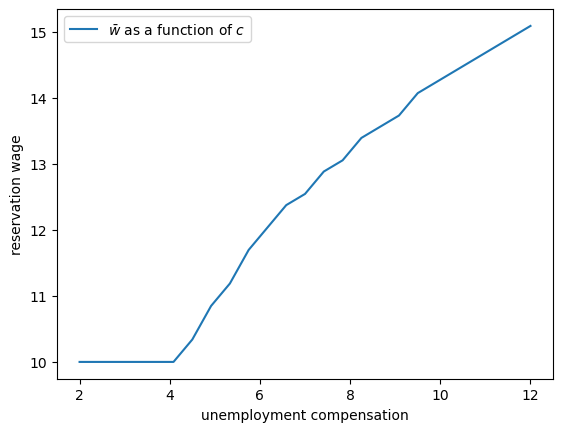
_images/fb6b35bc14ca1c1aa938e901c5f3cb4db4643fda50092dc59dc3ce80bbb08947.png

As expected, higher unemployment compensation causes the worker to hold out for higher wages.

In effect, the cost of continuing job search is reduced.

43.7.2. The Reservation Wage and Discounting#

Next, let’s investigate how \(\bar w\) varies with the discount factor.

The next figure plots the reservation wage associated with different values of \(\beta\)

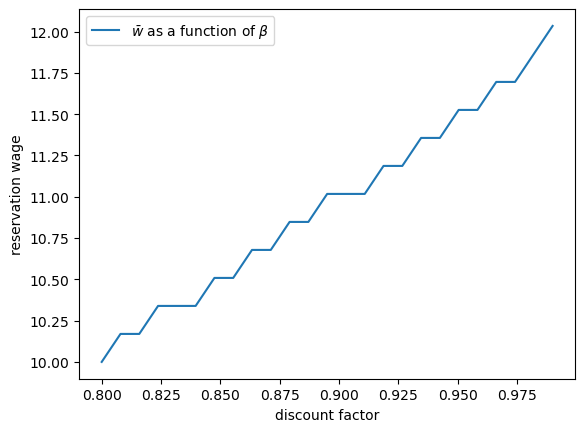
_images/f76dbd614c180a7ad1e080a5b4f733a708df1c6657d064c12a3459353a210d19.png

Again, the results are intuitive: More patient workers will hold out for higher wages.

43.7.3. The Reservation Wage and Job Destruction#

Finally, let’s look at how \(\bar w\) varies with the job separation rate \(\alpha\).

Higher \(\alpha\) translates to a greater chance that a worker will face termination in each period once employed.

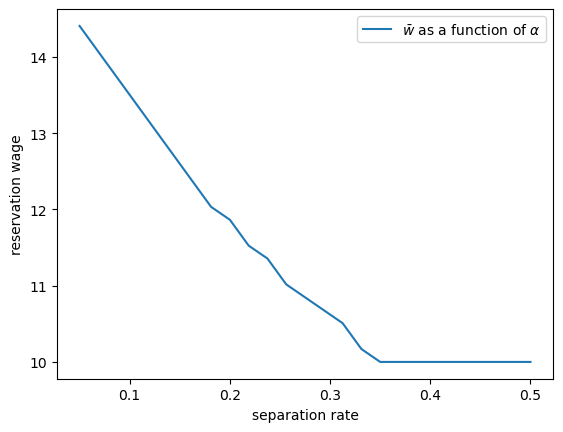
_images/7b5cf35639dbbee22403aaa3d932b5d3e8faa20c9941bba4402c0b8bca110c6f.png

Once more, the results are in line with our intuition.

If the separation rate is high, then the benefit of holding out for a higher wage falls.

Hence the reservation wage is lower.

43.8. Exercises #

Exercise 43.1

Reproduce all the reservation wage figures shown above.

Regarding the values on the horizontal axis, use

grid_size = 25
c_vals = jnp.linspace(2, 12, grid_size)         # unemployment compensation
β_vals = jnp.linspace(0.8, 0.99, grid_size)     # discount factors
α_vals = jnp.linspace(0.05, 0.5, grid_size)     # separation rate

Solution

Here’s the first figure.

def compute_res_wage_given_c(c):
    model = Model(c=c)
    w_bar = compute_reservation_wage(model)
    return w_bar

w_bar_vals = jax.vmap(compute_res_wage_given_c)(c_vals)

fig, ax = plt.subplots()
ax.set(xlabel='unemployment compensation', ylabel='reservation wage')
ax.plot(c_vals, w_bar_vals, label=r'$\bar w$ as a function of $c$')
ax.legend()
glue("mccall_resw_c", fig, display=False)
plt.show()

Here’s the second one.

def compute_res_wage_given_beta(β):
    model = Model(β=β)
    w_bar = compute_reservation_wage(model)
    return w_bar

w_bar_vals = jax.vmap(compute_res_wage_given_beta)(β_vals)

fig, ax = plt.subplots()
ax.set(xlabel='discount factor', ylabel='reservation wage')
ax.plot(β_vals, w_bar_vals, label=r'$\bar w$ as a function of $\beta$')
ax.legend()
glue("mccall_resw_beta", fig, display=False)
plt.show()

Here’s the third.

def compute_res_wage_given_alpha(α):
    model = Model(α=α)
    w_bar = compute_reservation_wage(model)
    return w_bar

w_bar_vals = jax.vmap(compute_res_wage_given_alpha)(α_vals)

fig, ax = plt.subplots()
ax.set(xlabel='separation rate', ylabel='reservation wage')
ax.plot(α_vals, w_bar_vals, label=r'$\bar w$ as a function of $\alpha$')
ax.legend()
glue("mccall_resw_alpha", fig, display=False)
plt.show()