45. Job Search IV: Fitted Value Function Iteration #

45.1. Overview #

This lecture follows on from the job search model with separation presented in the previous lecture.

In that lecture mixed exogenous job separation events and Markov wage offer distributions.

In this lecture we allow this wage offer process to be continuous rather than discrete.

In particular,

\[ W_t = \exp(X_t) \quad \text{where} \quad X_{t+1} = \rho X_t + \nu Z_{t+1} \]

and \(\{Z_t\}\) is IID and standard normal.

While we already considered continuous wage distributions briefly in Exercise Exercise 42.2 of the first job search lecture, the change was relatively trivial in that case.

The reason is that we were able to reduce the problem to solving for a single scalar value (the continuation value).

Here, in our Markov setting, the change is less trivial, since a continuous wage distribution leads to an uncountably infinite state space.

The infinite state space leads to additional challenges, particularly when it comes to applying value function iteration (VFI).

These challenges will lead us to modify VFI by adding an interpolation step.

The combination of VFI and this interpolation step is called fitted value function iteration (fitted VFI).

Fitted VFI is very common in practice, so we will take some time to work through the details.

In addition to what’s in Anaconda, this lecture will need the following libraries

!pip install quantecon

We will use the following imports:

import matplotlib.pyplot as plt
import jax
import jax.numpy as jnp
from jax import lax
from typing import NamedTuple
import quantecon as qe

Matplotlib is building the font cache; this may take a moment.

45.2. Model #

The model is the same as in the discrete case, with the following features:

Each period, an unemployed agent receives a wage offer \(w\)
Wage offers follow a continuous Markov process: \(W_t = \exp(X_t)\) where \(X_{t+1} = \rho X_t + \nu Z_{t+1}\)
\(\{Z_t\}\) is IID and standard normal
Jobs terminate with probability \(\alpha\) each period (separation rate)
Unemployed workers receive compensation \(c\) per period
Workers have CRRA utility \(u(c) = \frac{c^{1-\gamma} - 1}{1-\gamma}\)
Future payoffs are discounted by factor \(\beta \in (0,1)\)

45.3. The algorithm #

45.3.1. Value function iteration#

In the discrete case, we ended up iterating on the Bellman operator

(45.1)#\[ (Tv_u)(w) = \max \left\{ \frac{1}{1-\beta(1-\alpha)} \cdot \left( u(w) + \alpha\beta (Pv_u)(w) \right), u(c) + \beta(Pv_u)(w) \right\}\]

where

\[ (P v_u)(w) := \sum_{w'} v_u(w') P(w, w') \]

Here we iterate on the same law after changing the definition of the \(P\) operator to

\[ (P v_u)(w) := \int v_u(w') p(w, w') d w' \]

where \(p(w, \cdot)\) is the conditional density of \(w'\) given \(w\).

We can write this more explicitly as

\[ (P v_u)(w) := \int v_u( w^\rho \exp(\nu z) ) \psi(z) dz, \]

where \(\psi\) is the standard normal density.

Here we are thinking of \(v_u\) as a function on all of \(\mathbb{R}_+\).

45.3.2. Fitting#

In theory, we should now proceed as follows:

Begin with a guess \(v\)
Applying \(T\) to obtain the update \(v' = Tv\)
Unless some stopping condition is satisfied, set \(v = v'\) and go to step 2.

However, there is a problem we must confront before we implement this procedure: The iterates of the value function can neither be calculated exactly nor stored on a computer.

To see the issue, consider (45.1).

Even if \(v\) is a known function, the only way to store its update \(v'\) is to record its value \(v'(w)\) for every \(w \in \mathbb R_+\).

Clearly, this is impossible.

45.3.3. Fitted value function iteration#

What we will do instead is use fitted value function iteration.

The procedure is as follows:

Let a current guess \(v\) be given.

Now we record the value of the function \(v'\) at only finitely many “grid” points \(w_1 < w_2 < \cdots < w_I\) and then reconstruct \(v'\) from this information when required.

More precisely, the algorithm will be

Begin with an array \(\mathbf v\) representing the values of an initial guess of the value function on some grid points \(\{w_i\}\).
Build a function \(v\) on the state space \(\mathbb R_+\) by interpolation or approximation, based on \(\mathbf v\) and \(\{ w_i\}\).
Obtain and record the samples of the updated function \(v'(w_i)\) on each grid point \(w_i\).
Unless some stopping condition is satisfied, take this as the new array and go to step 1.

How should we go about step 2?

This is a problem of function approximation, and there are many ways to approach it.

What’s important here is that the function approximation scheme must not only produce a good approximation to each \(v\), but also that it combines well with the broader iteration algorithm described above.

One good choice from both respects is continuous piecewise linear interpolation.

This method

combines well with value function iteration (see, e.g., [Gordon, 1995] or [Stachurski, 2008]) and
preserves useful shape properties such as monotonicity and concavity/convexity.

Linear interpolation will be implemented using JAX’s interpolation function jnp.interp.

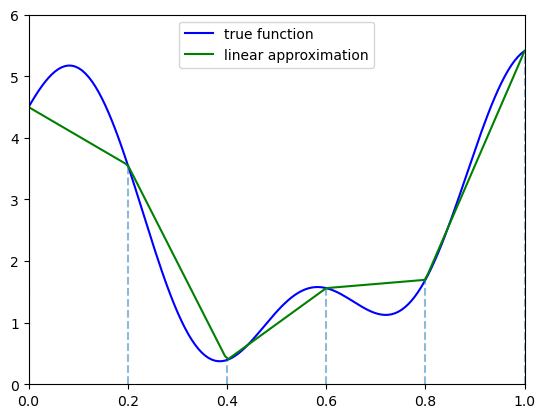
The next figure illustrates piecewise linear interpolation of an arbitrary function on grid points \(0, 0.2, 0.4, 0.6, 0.8, 1\).

def f(x):
    y1 = 2 * jnp.cos(6 * x) + jnp.sin(14 * x)
    return y1 + 2.5

c_grid = jnp.linspace(0, 1, 6)
f_grid = jnp.linspace(0, 1, 150)

def Af(x):
    return jnp.interp(x, c_grid, f(c_grid))

fig, ax = plt.subplots()

ax.plot(f_grid, f(f_grid), 'b-', label='true function')
ax.plot(f_grid, Af(f_grid), 'g-', label='linear approximation')
ax.vlines(c_grid, c_grid * 0, f(c_grid), linestyle='dashed', alpha=0.5)

ax.legend(loc="upper center")

ax.set(xlim=(0, 1), ylim=(0, 6))
plt.show()

_images/004d02c2821e33d9dff771a2d48cae86a6ee7194b6718e07f62cf85a631b4fe8.png

45.4. Implementation #

The first step is to build a JAX-compatible structure for the McCall model with separation and a continuous wage offer distribution.

The key computational challenge is evaluating the conditional expectation \((Pv_u)(w) = \int v_u(w') p(w, w') dw'\) at each wage grid point.

From the equation above, we have:

\[ (Pv_u)(w) = \int v_u(w^\rho \exp(\nu z)) \psi(z) dz \]

where \(\psi\) is the standard normal density.

We approximate this integral using Monte Carlo integration with draws from the standard normal distribution:

\[ (Pv_u)(w) \approx \frac{1}{N} \sum_{i=1}^N v_u(w^\rho \exp(\nu z_i)) \]

We use the same CRRA utility function as in the discrete case:

def u(c, γ):
    return (c**(1 - γ) - 1) / (1 - γ)

Here’s our model structure using a NamedTuple.

class Model(NamedTuple):
    c: float              # unemployment compensation
    α: float              # job separation rate
    β: float              # discount factor
    ρ: float              # wage persistence
    ν: float              # wage volatility
    γ: float              # utility parameter
    w_grid: jnp.ndarray   # grid of points for fitted VFI
    z_draws: jnp.ndarray  # draws from the standard normal distribution

def create_mccall_model(
        c: float = 1.0,
        α: float = 0.1,
        β: float = 0.96,
        ρ: float = 0.9,
        ν: float = 0.2,
        γ: float = 1.5,
        grid_size: int = 100,
        mc_size: int = 1000,
        seed: int = 1234
    ):
    """Factory function to create a McCall model instance."""

    key = jax.random.PRNGKey(seed)
    z_draws = jax.random.normal(key, (mc_size,))

    # Discretize just to get a suitable wage grid for interpolation
    mc = qe.markov.tauchen(grid_size, ρ, ν)
    w_grid = jnp.exp(jnp.array(mc.state_values))

    return Model(c=c, α=α, β=β, ρ=ρ, ν=ν, γ=γ, w_grid=w_grid, z_draws=z_draws)

def T(model, v):
    """Update the value function."""

    # Unpack model parameters
    c, α, β, ρ, ν, γ, w_grid, z_draws = model

    # Interpolate array represented value function
    vf = lambda x: jnp.interp(x, w_grid, v)

    def compute_expectation(w):
        # Use Monte Carlo to evaluate integral (P v)(w)
        # Compute E[v(w' | w)] where w' = w^ρ * exp(ν * z)
        w_next = w**ρ * jnp.exp(ν * z_draws)
        return jnp.mean(vf(w_next))

    compute_exp_all = jax.vmap(compute_expectation)
    Pv = compute_exp_all(w_grid)

    d = 1 / (1 - β * (1 - α))
    accept = d * (u(w_grid, γ) + α * β * Pv)
    reject = u(c, γ) + β * Pv
    return jnp.maximum(accept, reject)

Here’s the solver:

@jax.jit
def vfi(
        model: Model,
        tolerance: float = 1e-6,   # Error tolerance
        max_iter: int = 100_000,   # Max iteration bound
    ):

    v_init = jnp.zeros(model.w_grid.shape)

    def cond(loop_state):
        v, error, i = loop_state
        return (error > tolerance) & (i <= max_iter)

    def update(loop_state):
        v, error, i = loop_state
        v_new = T(model, v)
        error = jnp.max(jnp.abs(v_new - v))
        new_loop_state = v_new, error, i + 1
        return new_loop_state

    initial_state = (v_init, tolerance + 1, 1)
    final_loop_state = lax.while_loop(cond, update, initial_state)
    v_final, error, i = final_loop_state

    return v_final

The next function computes the optimal policy under the assumption that \(v\) is the value function:

def get_greedy(v: jnp.ndarray, model: Model) -> jnp.ndarray:
    """Get a v-greedy policy."""
    c, α, β, ρ, ν, γ, w_grid, z_draws = model

    # Interpolate value function
    vf = lambda x: jnp.interp(x, w_grid, v)

    def compute_expectation(w):
        # Use Monte Carlo to evaluate integral (P v)(w)
        # Compute E[v(w' | w)] where w' = w^ρ * exp(ν * z)
        w_next = w**ρ * jnp.exp(ν * z_draws)
        return jnp.mean(vf(w_next))

    compute_exp_all = jax.vmap(compute_expectation)
    Pv = compute_exp_all(w_grid)

    d = 1 / (1 - β * (1 - α))
    accept = d * (u(w_grid, γ) + α * β * Pv)
    reject = u(c, γ) + β * Pv
    σ = accept >= reject
    return σ

Here’s a function that takes an instance of Model and returns the associated reservation wage.

@jax.jit
def get_reservation_wage(σ: jnp.ndarray, model: Model) -> float:
    """
    Calculate the reservation wage from a given policy.

    Parameters:
    - σ: Policy array where σ[i] = True means accept wage w_grid[i]
    - model: Model instance containing wage values

    Returns:
    - Reservation wage (lowest wage for which policy indicates acceptance)
    """
    c, α, β, ρ, ν, γ, w_grid, z_draws = model

    # Find the first index where policy indicates acceptance
    # σ is a boolean array, argmax returns the first True value
    first_accept_idx = jnp.argmax(σ)

    # If no acceptance (all False), return infinity
    # Otherwise return the wage at the first acceptance index
    return jnp.where(jnp.any(σ), w_grid[first_accept_idx], jnp.inf)

45.5. Computing the Solution #

Let’s solve the model:

model = create_mccall_model()
c, α, β, ρ, ν, γ, w_grid, z_draws = model
v_star = vfi(model)
σ_star = get_greedy(v_star, model)

Next we compute some related quantities, including the reservation wage.

# Interpolate the value function for computing expectations
vf = lambda x: jnp.interp(x, w_grid, v_star)

def compute_expectation(w):
    # Use Monte Carlo to evaluate integral (P v)(w)
    # Compute E[v(w' | w)] where w' = w^ρ * exp(ν * z)
    w_next = w**ρ * jnp.exp(ν * z_draws)
    return jnp.mean(vf(w_next))

compute_exp_all = jax.vmap(compute_expectation)
Pv = compute_exp_all(w_grid)

d = 1 / (1 - β * (1 - α))
accept = d * (u(w_grid, γ) + α * β * Pv)
h_star = u(c, γ) + β * Pv
w_star = get_reservation_wage(σ_star, model)

Let’s plot our results.

fig, ax = plt.subplots(figsize=(9, 5.2))
ax.plot(w_grid, h_star, linewidth=4, ls="--", alpha=0.4,
        label="continuation value")
ax.plot(w_grid, accept, linewidth=4, ls="--", alpha=0.4,
        label="stopping value")
ax.plot(w_grid, v_star, "k-", alpha=0.7, label=r"$v_u^*(w)$")
ax.legend(frameon=False)
ax.set_xlabel(r"$w$")
plt.show()

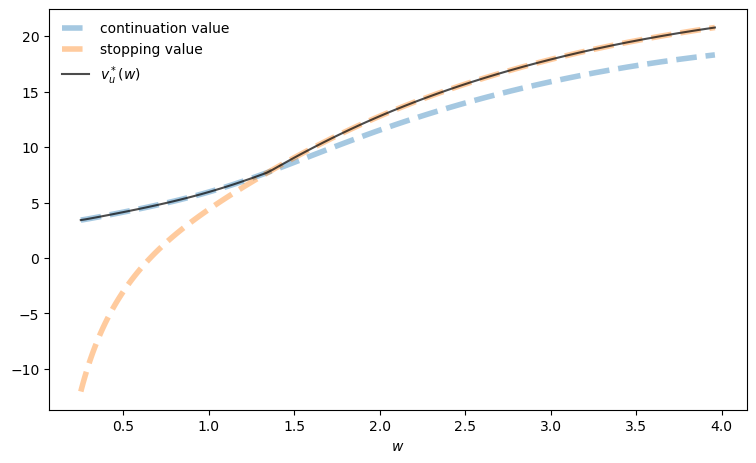
_images/6ed3da2841f1b349b3e9499d67d933ff72b1f1d336d582b3032b2362f0404334.png

The exercises ask you to explore the solution and how it changes with parameters.

45.6. Exercises #

Exercise 45.1

Use the code above to explore what happens to the reservation wage when \(c\) changes.

Solution

Here is one solution

def compute_res_wage_given_c(c):
    model = create_mccall_model(c=c)
    v_star = vfi(model)
    σ_star = get_greedy(v_star, model)
    w_bar = get_reservation_wage(σ_star, model)
    return w_bar

c_vals = jnp.linspace(0.0, 2.0, 15)
w_bar_vals = jax.vmap(compute_res_wage_given_c)(c_vals)

fig, ax = plt.subplots()
ax.set(xlabel='unemployment compensation', ylabel='reservation wage')
ax.plot(c_vals, w_bar_vals, label=r'$\bar w$ as a function of $c$')
ax.legend()
plt.show()

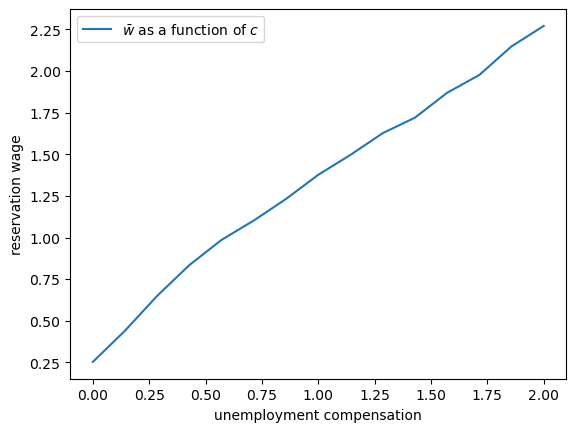
_images/ce32a4f0b218573fb7d1233caf24dda7d0fedc4faa31e1c177bdc19f689dc693.png

As unemployment compensation increases, the reservation wage also increases.

This makes economic sense: when the value of being unemployed rises (through higher \(c\)), workers become more selective about which job offers to accept.

Exercise 45.2

Create a plot that shows how the reservation wage changes with the risk aversion parameter \(\gamma\).

Use γ_vals = jnp.linspace(1.2, 2.5, 15) and keep all other parameters at their default values.

How do you expect the reservation wage to vary with \(\gamma\)? Why?

Solution

We compute the reservation wage for different values of the risk aversion parameter:

γ_vals = jnp.linspace(1.2, 2.5, 15)
w_star_vec = jnp.empty_like(γ_vals)

for i, γ in enumerate(γ_vals):
    model = create_mccall_model(γ=γ)
    v_star = vfi(model)
    σ_star = get_greedy(v_star, model)
    w_star = get_reservation_wage(σ_star, model)
    w_star_vec = w_star_vec.at[i].set(w_star)

fig, ax = plt.subplots(figsize=(9, 5.2))
ax.plot(γ_vals, w_star_vec, linewidth=2, alpha=0.6,
        label='reservation wage')
ax.legend(frameon=False)
ax.set_xlabel(r'$\gamma$')
ax.set_ylabel(r'$w^*$')
ax.set_title('Reservation wage as a function of risk aversion')
plt.show()

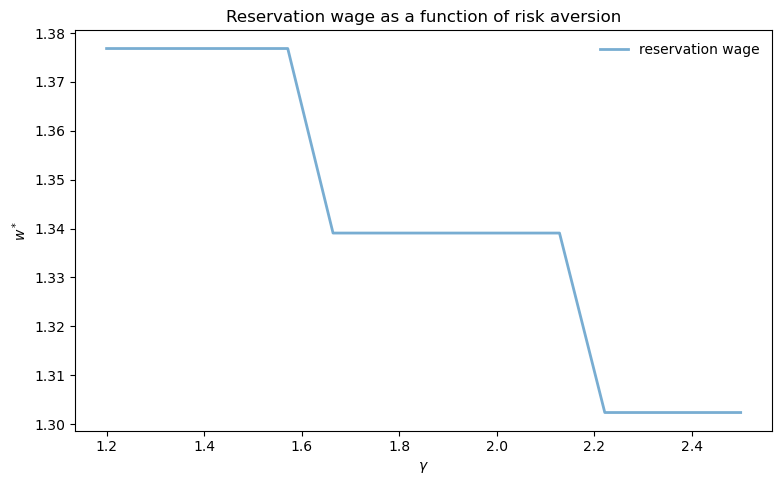
_images/d35e3db07f70566d825e6dc4b4c4fcf94ffb910a75cbf3f62084e1cc98a3f9fd.png

As risk aversion (\(\gamma\)) increases, the reservation wage decreases.

This occurs because more risk-averse workers place higher value on the security of employment relative to the uncertainty of continued search.

With higher \(\gamma\), the utility cost of unemployment (foregone consumption) becomes more severe, making workers more willing to accept lower wages rather than continue searching.

45. Job Search IV: Fitted Value Function Iteration#

45.1. Overview#

45.2. Model#

45.3. The algorithm#

45.3.1. Value function iteration#

45.3.2. Fitting#

45.3.3. Fitted value function iteration#

45.4. Implementation#

45.5. Computing the Solution#

45.6. Exercises#

45. Job Search IV: Fitted Value Function Iteration #

45.1. Overview #

45.2. Model #

45.3. The algorithm #

45.4. Implementation #

45.5. Computing the Solution #

45.6. Exercises #